複雑な形状の空間で、熱はどのように伝わるのか

熱は一般に、「熱方程式」と呼ばれる次の式に従って伝わっていくことが知られている。

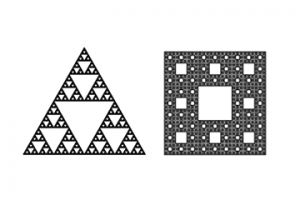
図1：フラクタルの典型例であるシェルピンスキーガスケット（左）とシェルピンスキーカーペット。出典：熊谷隆教授、第35回(平成29年度)大阪科学賞 受賞記念講演会レジュメhttp://www.ostec.or.jp/pln/pri/kagaku/29-1.pdf　以降の各図も同様。

（α：熱伝導係数、T：温度）

しかし、これは通常の図形や空間、いわゆるユークリッド空間においての話である。より複雑な図形や空間では、上記の式とは異なる伝わり方、すなわち「異常拡散」を起こすことがわかってきた。そのような複雑な図形の好例がフラクタルである。

フラクタルとは、1970年代にフランスの数学者マンデルブロによって提案された幾何学の概念だ。図形の一部分と全体の間に相似性がある図形のことで、海岸線、雲の形、結晶構造、複雑なネットワークの構造など、現実のさまざまなところに表れる。
フラクタルの概念が知られるようになると、まず、その上を熱がどう伝わるのかが物理学的に研究されるようになっていった。そして80年代後半に入ると、数学者たちによって、数学的な解析の研究が始まった。

自身の研究について柔らかい口調で説明する熊谷教授。

その研究は、シンプルな図形から始まり、より複雑なフラクタルや、フラクタルではないがフラクタルに近い図形での解析へと進んでいった。その理論を、フラクタルではないよりランダムで複雑な図形へ拡張し、さらにはあらゆる複雑な形状のモノの熱伝導を数学的に解明しようという方向に向かうのは自然だろう。
しかし、複雑なフラクタルにおける熱伝導の解析には、多くの未解決問題が残り、研究はなかなか進まなかった。そうしたなかで熊谷教授は、フラクタルの熱伝導に関して基礎を固める研究を重ね、重要な未解決問題も解決した。加えて、よりランダムな系における異常拡散現象の解析にも取り組んできた。

熱を伝える粒子のランダムな運動

フラクタルは、一般的なユークリッド空間と本質的にどう違うのか。そしてフラクタルの熱伝導について考えることにはどんな意味があるのか。熊谷教授はこう話す。
「たとえば普通の三次元空間は、どこを見ても同じです。すなわち空間を平行移動させても状況は変わらない。一方、フラクタルなど、私たちが扱う複雑な図形というのは、場所によって性質が異なるため、平行移動させると状況が変わってしまう。すなわち、“平行移動不変性”がありません。ただしフラクタルは、拡大縮小によって形が一緒になるという自己相似性がある。そのため、全くランダムな図形よりは扱いやすい。それゆえ、まずはフラクタルで熱伝導の解析を行い、それをステップとして、よりランダムな図形の解析へと進んでいくのです」

熱伝導を数学的に解析するには、確率論の方法が用いられる。というのも、熱が伝わるというのは、物質中での粒子のランダムな振動によって生じる現象だからだ。先述の熱方程式は、粒子などの拡散に関する拡散方程式と数学的には同じものだ。それゆえ、微小粒子のランダムな動きを確率論の方法で記述することで、熱の伝導を考えることができるのである。
熱伝導の具体的な解析において、重要な意味を持ってくるのが「ブラウン運動」と呼ばれる現象だ。ブラウン運動とは、液体などの溶媒の中に浮かぶ微粒子が不規則に動く運動を指す物理学の用語だ。数学においては、粒子のランダムな動き（＝ランダムウォーク）を連続的に厳密に記述したモデルを意味する。フラクタルな図形で粒子がブラウン運動する状況を記述すれば、それがフラクタル上で熱が伝わる様子を解析することへとつながるのである。

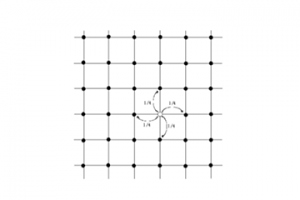
図2：ユークリッド空間におけるランダムウォークの例。

ここで、フラクタルとの対比で、ユークリッド空間上でのブラウン運動についてまず考えてみたい。
「左の図のような正方格子上の1点に粒子があり、一秒後には、上下左右のいずれかの方向に、それぞれ1/4の確率で動くランダムウォークを考えます。このメッシュを小さくした極限を考え、メッシュの一辺の長さを 2^-nとしてn を無限大にすると連続な空間（ユークリッド空間）になります。その場合、粒子は1 秒間に2^-nずつ動くことになるわけですが、nを無限大にすると2^-nは0になり、粒子は全く動かないことになってしまいます。そこで、実際に粒子が動いてブラウン運動するように、時間の適切なスピードアップを試みます。このとき、時間を4ⁿ = 2²ⁿでスピードアップすると、ブラウン運動に収束することがわかっています」

ここで重要なことが2つある。ひとつは、“4ⁿ”でスピードアップさせるとブラウン運動に収束すること。そして、4ⁿ＝2²ⁿであり、2を底とした時の指数が“2n”であることだ。この指数のｎの係数に当たる部分（ここでは2）は「ウォーク次元」と呼ばれ「d_w」と書く。このd_wの値が、粒子がどう拡散するかに大きく関係しているのである。
通常のユークリッド空間では、d_wの値は2となることが知られている。それが、ユークリッド空間における熱方程式（冒頭の式）の右辺が「二階微分」になっていることと深い関係がある。二階微分とは、微分によって導かれた「導関数」を、さらに微分した関数のことだ。熱方程式の右辺は、まさにこの二階微分の形をしているのである。また、d_wが2以外となる熱拡散現象を「異常拡散」という。

フラクタルでの粒子の異常拡散

ここからが、フラクタルでのブラウン運動についてだ。フラクタルの典型例である「シェルピンスキーガスケット」（図1左図参照）を題材とするのだが、そのままでは計算が複雑になりすぎるため、図3のようにガスケットを近似したグラフで計算を進めていく。
このグラフ上で、ある点にいる粒子が1 秒後に等確率で隣の点に動くようなランダムウォークを考える。正方格子と異なるのは、動いた先の4点が、正方格子の場合のように対等ではないことである。

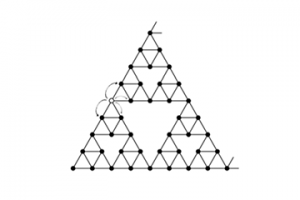
図3：シェルピンスキーガスケットを近似したグラフ。

ここでもグラフを縮小し、一辺の長さを2^-nとして n を無限大にすると、無限に延びたガスケットができる。このグラフでもやはり、粒子の動きをブラウン運動に収束させるには時間のスピードアップが必要だ。その値は“5ⁿ”であることが、1980 年代後半に数学的に厳密に示されている。5ⁿは、2を底とする指数で表現すると、“2^{n log 5/log 2}”となる。
「この結果は、ガスケットの熱伝導におけるウォーク次元d_wがlog 5/log 2であることを示しています。d_wが2以外の値をとることから、フラクタルでは、ユークリッド空間で起きる拡散とは別の異常拡散現象が起きることがわかるのです」

d_wの値は、熱伝導の速さについても教えてくれる。
「両者の間には相関関係があることがわかっています。d_wが大きければ長時間での粒子の拡散は遅い、すなわち熱伝導も遅い。d_wが小さければ拡散が速い、すなわち熱伝導も速いということです。」

このように、熱伝導の解析においてウォーク次元d_wは重要な意味を持つ。
「d_wの値は、いくつかの具体的な図形については知られています。複雑な図形のd_wを得られれば、その図形上の熱伝導の仕方が見えてきます。そこまでの解析を、いかなる複雑な図形でもできるようになることが、私たちの研究の目指すところの一つです。とはいえ、複雑すぎる図形にいきなり取り組むことはできません。その前段階として、まずフラクタルの解析を行い、よりランダムな図形へと研究を進めています」

2時間ほどのインタビューの間、熊谷教授は白板を何度も消しては書き加えながら、理論を丁寧に説明してくれた。

理想的なフラクタルから、さらにランダムな図形へ

一連の研究の末、熊谷教授は共同研究者とともに、フラクタルのなかでも比較的理想的な形をした図形における熱方程式の基本解（熱核）が次のような評価を持つことを示した。これは、ガスケットの場合などに知られていた結果の拡張である。

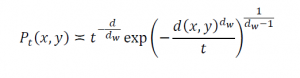
ここで、ウォーク次元d_wの値が2の時、式は以下のようになる。

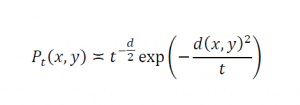
この式の右辺は「ガウス核」と呼ばれ、確率統計では一番典型的な熱伝導の形である。すなわち、ガウス核はd_wの値が2である場合の、熱核の特殊なケースである。言い方を変えれば、上の熱核評価は、ガウス型の評価をd_wが2より大きい値になるような異常拡散の場合にも当てはまるよう拡張した、より汎用的な式なのである。

続いて熊谷教授は、共同研究者とともに、理想的なフラクタルの解析を、完全にはフラクタルとはいえない図形にも応用可能であることを証明した。その理論は「摂動安定性理論」と呼ばれる。
「たとえば、遠くからはフラクタルのように見えるけれども、近くでその一部を見るとユークリッド空間的であるという図形が現実には多くあります。ジャングルジムが、遠くから見れば大きな立方体に見えるけれど、近くで一部分だけを見ると円柱である、というように。そのような図形の熱伝導を考える場合、拡散する距離が小さい短時間の場合はユークリッド空間として扱えるものの、時間が長くなり、拡散距離が大きくなったらフラクタル的に扱う必要性が出てきます。その場合に適したような、時間に応じてd_wが変わるような式も求められています。そのように、理想的な状態から少し外れた形でも、熱の伝わり方は理想的な形の時と大きくは変わらず、同様に考えられるというのが『摂動安定性』です。それにより、さらにランダムな形状でも解析ができるところまで、研究が進んでいます。」

人との関わりを通じて、自分の研究テーマがきっと見つかる

数学では、何かの証明を考えるのに長い時間を費やすという。考えるときは、基本的に紙と鉛筆を使うのだそうだ。

熊谷教授の研究は、純粋な数学でありながら、現実の問題ともつながりが強く、応用範囲も広いのが特徴だ。
「熱が伝わりにくい材料をつくるには、d_wが出来るだけ大きくなるような物質をつくればよい。それにはどのような分子構造の物をつくればよいか。そうしたことについて、企業の人と議論することもあります。材料の形から、熱伝導がどうなるかを予測できるぐらいに理論を突き詰めることができれば、新しい材料をつくるとき、どのような分子構造の物質を使えば良いかを考える情報を提供できるようになります」
また、複雑な図形上の熱伝導の解析は、ビッグデータやネットワークなど現代社会に大きくかかわる問題の解析にもつながるという。基礎理論と応用の両面に取り組めるこの分野は、今後ますます発展していく可能性がありそうだ。

熊谷教授が、今の研究に至った経緯も紹介しておきたい。
「大学に入った当初はクラシカルなテーマに憧れていました。ところが、理論を深めていくとどんどん抽象化され、自分がどのような研究を目指すのかが見えにくくなりました。その一方で大学の後半には、確率論の面白さに気付き始めました。そんなとき、当時はまだ比較的新しかったフラクタルについて学ぶ機会がありました。演習を担当しておられた藤田岳彦先生（現・中央大学教授）から、『確率だったらフラクタルもできるし、解析もできる』と言われたことが、この方向に進む一つのきっかけとなりました。その後、渡辺信三先生（現・京都大学名誉教授）に師事し、確率論の分野で研究を始めました。フラクタル上の解析学を創始された楠岡成雄先生（現・東京大学名誉教授）や木上淳先生（現・京都大学教授）も当時は京都周辺におられ、研究環境に大変恵まれていたことは、自分の研究を進める上でとても大きかったと思います」

熊谷教授は、確率論の面白さを次のように語る。
「確率論は、粒子が動いてるというダイナミックな感覚があって直感が働きやすいのが面白さの一つだと感じます。また、純粋数学でありながら応用範囲が広いのも魅力です。純粋数学もやりたいし、でもその応用として社会とも関わって違った刺激も得たい。そういう人にとっては、確率論はとても魅力的な分野だと思います」

熊谷教授の著作。『新しい解析学の流れ　確率論』（共立出版、2003年刊）は、理工系の学部3・4年生から大学院初年度の学生を主な対象として書かれた確率論の入門書。2014年刊の英書では、複雑な図形におけるランダムウォークの研究をまとめた。

熊谷教授は、一連の研究成果によって、フンボルト賞や井上学術賞をはじめ、数々の権威ある賞を受賞している。そのように大きな業績を上げるにあたっては、さまざまな出会いが重要だったと振り返る。その経験から、若い人たちにも、人との出会いを求めて、積極的に動くことの大切さを伝えたいという。
「私は若いころから、部屋で黙々と論文を読むだけでなく、人と会って議論をしながら考えることを大切にしていました。人との関わりを通じて、面白そうなテーマを探って自分なりの方向性を見つけてきたように思います。これも、自分の研究テーマを見つけるひとつの方法だと思います。わりと早い段階から海外に出たことも、私の研究に大きな影響を与えています。自分でしっかりと勉強して考えを深めることがまず大事であるのは当然ですが、その上で、外とも積極的に関わっていくことはプラスになるはずです。ぜひこれだという分野を見つけて、突き進んでもらえたらと思います」

【取材・文：近藤雄生／撮影：吉田亮人】