

2016年2月、アメリカの重力波望遠鏡LIGO(レーザー干渉計重力波天文台)が重力波を検出に成功したと発表した。
重力波とは、時空の歪みによって生じる波で、“時空のさざ波”と呼ばれる。その存在は確実視されながらも誰も観測できずにいた。それが初めて捉えられたのだ。
LIGOが検出したデータの解析には、「数値相対論」と呼ばれるコンピュータによる数値計算が大きな役割を果たしている。重力波は今後さらに観測事例が増えていく見通しで、数値相対論の役割はますます大きくなっていくと考えられている。
今回は、数値相対論を研究する京都大学基礎物理学研究所の柴田大教授を訪ねた。重力波とは何か、そして数値相対論がどう関わっているのか。最新の事情を伺った。
「LIGOが重力波の信号を捉えたのは2015年9月のことです。これは本当に歴史的な観測です。重力波の観測そのものが初めてなら、連星として回る2つのブラックホールを人間が確認したのも初めてです(詳しくは後述)。シグナルもとてもはっきりとしていて、重力波であることはまず間違いないといえる圧倒的な成果です。そしてこの観測は、数値相対論が重力波の研究に必須の道具であることを初めてはっきりと示した例でもあるのです」
柴田教授は、冒頭、興奮気味にそう語った。
重力波は、いまからちょうど100年前の1916年に、一般相対性理論(以下、一般相対論)から導かれる現象として、アインシュタインがその存在を予言した。ひとことでは“時空のさざ波”といわれるが、もう少し説明が必要だろう。

一つひとつの質問に丁寧に答えてくださる柴田教授。
一般相対論では、質量のある物体が存在するとその付近の時空(時間と空間を合わせた概念)が歪むと考える。その歪みに沿って物体が動くことが重力の正体であるとされるが、物体が加速度運動するとその歪みが水面の波紋のように空間を伝播する。それが重力波なのである。重力波を観測することは、一般相対論の正しさを裏付ける新たな証拠になるととともに、私たちが宇宙を観測する新たな手段を得ることを意味する。それゆえとても意義が大きい。
重力波の存在は1980年代に間接的には証明されていたが、直接観測はかなわないままだった。質量のあるものが加速度運動をすれば常に重力波が生じるが、そもそも強い波ではないため感知・観測するのが難しいのだ。
私たちが観測できるほど大きな重力波が生じるためには、とても高密度で質量の大きな物体が激しい加速度運動をする必要がある。そうした運動の最も有力な候補となるのが、中性子星やブラックホールといった大質量の天体2つが、互いに力を及ぼし合いながら近づき合体する現象である。すなわち、「連星中性子星の合体」、「連星ブラックホールの合体」である(互いに力を及ぼし合って運動する2つの天体を「連星」と呼ぶ)。
ちなみに中性子星とは、大質量の恒星がその寿命の最後に起こす超新星爆発のあとで生じる星で、主に中性子からできている。質量は太陽の1.5~2倍程度。一方、ブラックホールは、大質量の恒星の中でもとりわけ重い恒星(太陽の30倍以上の質量を持つもの)が強い重力のため崩壊すると誕生する天体である。恒星が重力崩壊して誕生するブラックホールの質量は太陽の5~100倍程度と推定されている。

連星をなす二つの天体が互いに渦を巻くように回転しながら接近し、重力波が放出されるイメージ図。重力波は、赤い渦状の線で示すように、波紋のように広がっていく。(図:京都大学基礎物理学研究所 川口恭平氏作成)
近接連星(天体同士の距離が十分に近づいた連星のこと)をなす2つの中性子星またブラックホールは、互いに渦を巻くように回転する。そのとき重力波が放出され、その分だけエネルギーと角運動量を失うため、さらに互いの距離が近づいていく。そして近づくにつれて速度が大きくなり、最終的には光速の数分の1程度にまで加速された上で合体する。そのとき膨大なエネルギーが放出されるとともに強い重力波が生じるのである。
LIGOが観測した重力波は、2つのブラックホールの合体によって発生したと発表された。2つのブラックホールはそれぞれおよそ太陽の36倍と29倍の質量を持ち、数十億年の間、互いの周りを回り続けた末、合体したと推定されている。合体の直前には、宇宙にあるすべての恒星が放出するエネルギーの合計の約50倍ものエネルギーが放出されたと計算されている。これまで観測された天体現象の中でもっとも高エネルギーな出来事である。
しかし、検出器が重力波らしき信号を検出したとはいえ、なぜそれが、上記のようなブラックホールに由来するとわかるのだろうか。ブラックホールはその姿が見えるわけでもなく、重力波の信号以外何も情報はないのである。じつはここで力を発揮しているのが数値相対論なのである。
「数値相対論とは、連星中性子星や連星ブラックホールのような強い重力下で起きる動的な現象を、一般相対論の数値計算によって解き明かすことを目的とした研究分野です」
そう柴田教授は説明する。
一般相対論においては、空間は曲がり、時間は速くなったり遅くなったりする(つまり、空間も時間も絶対的なものではなく、変化する)。ただしその効果が無視できない大きさで現われるのは、重力が十分に強い環境や、物体が光速に近い速度で動いている場合である。私たちが普段生活している環境は、重力も速度も十分に小さいため一般相対論を意識する必要はないのだが、宇宙で起こる多くの現象は一般相対論によって考える必要があるのである。

研究には基本的に一人で取り組む。その舞台となるのがこの研究室だ。室内にはパソコン数台があるだけですっきりしている。
一般相対論の基本方程式は「アインシュタイン方程式」である。この方程式は、空間の曲がり具合が時間とともにどう変化していくかを定式化したものだ。つまりこれを解けば、たとえば連星ブラックホールが合体するときにその周りの空間の曲がり具合がどう変化していくかが計算できるのである。
ただし、アインシュタイン方程式は「非線形連立微分方程式」と呼ばれる非常に複雑な式になり、解析的に解を求めることが不可能である。つまり、既知の関数などをそのままの形で計算して厳密な解を得ることができない。そこで、「数値的な解法」を取り入れることが不可欠となり、「数値相対論」という分野が生まれたのだ。
「数値的な解法」とは一般に、微分を差分に置き換えて解くことである。すなわち、変化率を求めるために本来微分すべきところを引き算による近似的な手法で代用して解くのである。厳密解は得られないが、原理的には差分の領域を細かくしていくことで厳密解に限りなく近づける。必要に応じて精度はこちらで制御できるため、この方法でも十分に正確な解が得られるといえる。
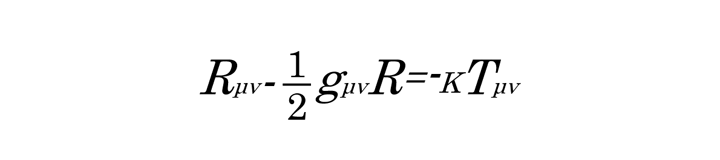
アインシュタイン方程式。左辺は、時空の曲がり具合を示し、右辺は物質の分布を表す。つまり、物質の分布を決めれば周囲の空間の曲がり具合が決まる。各記号はRμν :リッチテンソル、R:スカラー曲率、gμν :計量テンソル、Tμν :エネルギー・運動量テンソル、κ:アインシュタインの重力定数(ニュートンの重力定数Gとの間に次の関係があるκ = 8πG/c4 、c:光速、π:円周率)。これをx,yなどの変数と一般的な演算記号を使って書いていった場合、変数、式ともに10個ほどになり、「一つの式だけでノート1、2ページにも及ぶ複雑な式になる」(柴田教授)という。
数値相対論の研究が始まったのは、1960年代から70年代のことである。ブラックホールや中性子星、連星中性子星といった一般相対論的とされる天体や宇宙現象が実際に観測されるようになったのを受けてのことだ。
そして90年代に入ると世界各地で一気に研究が進展する。アメリカのLIGOをはじめとする大型重力波望遠鏡の建設が開始されたことで、重力波の正体を理論的に予言しておくことが必要不可欠になったからだ。そのためには、数値相対論によってアインシュタイン方程式を解かなければならないのである。
「それまでは、アインシュタイン方程式を解くための方法が十分に確立されていなかったため、研究は、興味ある天体現象に対してどうやって定式化するかというところに留まっていました。それがようやく90年代に入り、実際に方程式を解くことができるようになっていったのです」

コンピュータプログラムによるシミュレーションが、数値相対論研究の大きな柱となる。「大きな実験装置などは使いませんが、シミュレーション用のプログラムを自作することは、自分で実験装置を作って実験をするということでもあります。数値計算は、基本的には理論研究に近いですが、その意味では実験的な要素も強くあるといえます」と柴田教授。

アインシュタイン方程式を数値計算のための形に書き直した一部。具体的な変数を用いて一つ一つ書いていくため膨大な長さの方程式となる。
アインシュタイン方程式を解く難しさとは一体どのような点にあるのだろうか。そのさわりだけでも紹介しよう。
「まず、この方程式には書き方が無数にあります。これは、一般相対論では、時間も空間も絶対ではなく自由に選べるものであり、絶対的な時間・空間座標が存在しないからです。ゆえに、自分で時間軸を決めたり、時間一定となる空間面を張ったりしなければなりません。うまく座標をとらないと解くことが不可能になるため、扱う現象の物理学的な意味をよく理解した上で適切な座標をとり、かつ、その座標に適した式の書き方をしなければなりません。変数は10個ほど出てきますが、座標をうまくとれば、ある一群は消えてくれるということが起きる一方、うまくやらないと絶対に解けない状態になることもあります」
座標軸の採り方はアインシュタイン方程式の最も難しいところでもある。ただ、研究が進むにつれて、座標をどう採ればいいかという理論は確立されてきた。そのため、いまはこの点で頭を悩ます必要はなくなったという。
また、アインシュタイン方程式を解くときには、満たさなければならない「拘束条件」がある。数値的に解いていくと、その過程で拘束条件を満たさなくなり計算が破綻してしまうという問題があったが、その問題を回避する定式化の方法もいまでは確立されている。ちなみにその定式化手法の代表的なものは、考案者の名をとって「BSSN (Baumgarte-Shapiro-Shibata-Nakamura)形式」と呼ばれるが、その名前からわかる通り、考案者の一人が柴田教授なのである。
こうした数々の研究者の尽力により、方程式を解く上での大きな問題は解決していった。そこにはコンピュータの性能の向上も大きく寄与している。計算速度が上がったということのみならず、コンピュータの性能が上がることで多様な実験的シミュレーションが可能になり、それによって、方程式を解くための技術的な問題点の多くが解決したという。つまり、コンピュータが発展したことによって、数値相対論の理論そのものも進歩したのである。
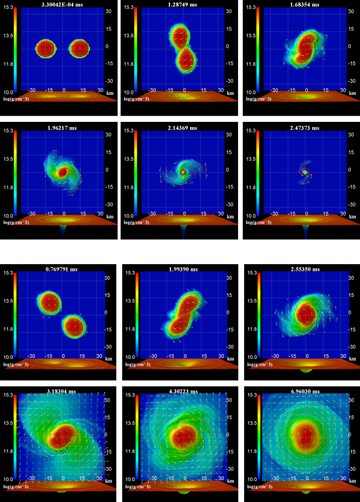
連星中性子星が合体してブラックホールが誕生するケース(上)と大質量の中性子星が誕生するケース(下)それぞれのシミュレーション例。連星は互いに100万キロぐらい離れた状態から数億年かけて近づいて合体する。1000キロぐらいまでに近づくと数十分で合体まで至り、残り30キロぐらいの距離では互いに相手の周りを一周するのに1ミリ秒かからないほどの速度になる。(図:柴田教授提供)
そうしてようやく、アインシュタイン方程式を実際の宇宙現象に適用し、数値相対論を用いて解いてシミュレーションする準備が整っていった。
そもそも数値相対論の最大の目的は、重力波について理論的な理解を進めることであった。重力波の発生源として、連星中性子星や連星ブラックホールの合体が有望な天体現象であることはわかっていたので、数値相対論の最重要課題は、それらの合体現象をシミュレーションし、発生する重力波の波形を正確に予言することになっていった。
2000年代後半に入ると、まず、連星ブラックホールの合体のシミュレーションが飛躍的に進んでいった。欧米の多くのグループによって研究がなされた結果、連星ブラックホールが合体するとその直後に新たに定常ブラックホールが誕生するというシナリオが確立し、その典型的な重力波の波形パターンも理解されるようになった。
その一方、より難しいのが連星中性子星の合体であった。ブラックホールが真空の時空を扱えばいいのに対して、中性子星は、内部の物質の物理的情報を正しく考慮する必要があるためだ。
柴田教授は、連星中性子星の合体の研究に長年取り組んできた。ブラックホールのシミュレーションが各地で行われていたのと同じころ、世界で初めて、連星中性子星の合体のシミュレーションに成功し、その研究に継続的に取り組んでいる。
「中性子星は謎が多く、その状態を記述する“状態方程式”がいまなおはっきりわかっていません。候補となる状態方程式が複数存在あり、それらを用いて多数のシミュレーションをしている段階です」
柴田教授は、この10年以上の間、さまざまなモデルのシミュレーションを試みてきた。連星中性子星の合体後に、ブラックホールが誕生する場合や大質量の中性子星が誕生する場合など複数のケースにおいて、発生する重力波を計算し、さまざまな知見を得てきている。
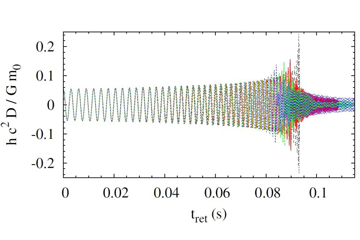
連星中性子星の合体のシミュレーションから得た重力波の波形。4つの異なる状態方程式から導かれる計算結果を重ねたもの。実際に重力波が観測されたとき、たとえばこの4つのどの波形に近いかを調べることでどの状態方程式がより正しいかが検証できる。(図:柴田教授提供)
なかでも近年特に力を入れて行ってきたのが、連星中性子星の合体時に起きるニュートリノ放射や磁気流体過程といった現象はとりあえず無視しつつも、観測事実と矛盾しない、現実的な状態方程式にもとづいたシミュレーションだ。それにより得た最も重要な知見の一つについて、柴田教授は次のように語る。
「典型的な質量の連星中性子星(2つの中性子星の質量の総和が太陽の2.7倍程度)が合体する場合、即座にブラックホールになることはなく、まず質量の大きな中性子星が新たに誕生します。そしてしばらく経ってから(といっても数十~数百ミリ秒程度という短い時間)、自らの重力によってつぶれてブラックホールになっていくと予想されます」
シミュレーションは、観測結果と比較してこそその意味が明確になる。それゆえ数値相対論による仕事が完結するには、とにかく重力波が実際に観測される必要がある。しかし、重力波の信号はまだほとんど検出されていない。その最初のものが、2016年2月に発表されたLIGOによる観測だったのである(観測は2015年9月)。
LIGOは今後改良が加えられ、最終的には2015年の観測時に比べて3倍ほど感度が上がる予定だという。つまり、現状より3倍遠くの場所で発生した重力波まで観測できるようになる。
「これから重力波の観測事例は間違いなく増えるはずです。観測すべき現象自体は、宇宙全体で見たら頻繁に起きているからです。たとえば連星中性子星の合体は、今後年間10回~100回といった頻度で観測されるようになるかもしれません」
日本でも間もなく、重力波の観測装置が運転を始めることになる。それが、岐阜県飛騨市神岡町で建設が進んでいる「KAGRA(大型低温重力波望遠鏡)」だ。2016年3月に試験運転をはじめ、2018年ごろから本格的な観測が始められる予定であるという。
KAGRAは神岡鉱山跡地の地下200メートルに建設されている。そのため地面振動が極めて少なくノイズが大きく減じられる。また検出器をマイナス253℃にまで冷却することで、熱雑音の低減も実現する。そうした試みによって感度の向上が期待される。

ご自身の近著と。研究者を目指す学生へのメッセージをお願いすると「何かに興味をもったら、とにかくその関連書を数多く読んだりしてその分野を深く探っていくことが重要です。積極的に動けば、やりたいことはきっと見えてきます。研究者を目指す人には、その努力をしてほしいと思います」と柴田教授。
ただ、LIGOがすでに重力波の初観測を実現させ、さらに改良がなされているなか、KAGRAの果すべき役割はどういったものであるのかは気になるところだ。その点を尋ねると柴田教授は、「KAGRAが完成する意義は極めて大きい」と答えた。
「重力波がどこから来たのかを知るためには、異なる場所にある最低3台の検出器で観測し、観測の時間差を測ることが必要です。LIGOは検出器が2台しかありません。今回の観測では、偶然2台でも推定できる方向から信号がやってきたという幸運がありましたが、いつもそうはいきません。そのため、完成すれば現状では世界で3台目の検出器となるKAGRAの役割は大きいのです。イタリアにもVIRGOという検出器があり、現在は改良工事のために運転が止められていますが、こちらの運転が再開すればさらに多くの情報が得られるようになります。確かに、重力波を初めて観測したという点でLIGOの業績の持つ意味が大きいことは間違いありません。しかし、重力波の研究は今後、国際協力があってこそ進んでいくものです。LIGOの観測によってKAGRAやVIRGOの関係者もみな活気づいたのではないかと私は思っています」
これから数年の間に重力波の解明は大きく進んでいくだろう。その中で数値相対論が果す役割もますます大きなものとなっていくはずだ。
重力波という、いま最もホットともいえる分野を最前線で研究する柴田教授だが、学生時代は、自分に宇宙を研究していくだけの能力があるかはわからないと感じていたという。

基礎物理学研究所の湯川記念館の前で、佐々木節所長(左)と。柴田教授も学生時代、佐々木所長に教わっている。「佐々木さんはいつも『数値計算の結果をそのまま信用しちゃいかん』とおっしゃっていました。つまり、計算結果が得られても、それが必ず物理学的な考察によって説明出来なければ意味がないと。数値計算は決して、単なるコンピュータシミュレーションではありません。物理学の深い理解が必須の分野です」
「宇宙には幼少期から一貫して興味があり、東京工業大学理学部の物理学科へ進んで本格的に宇宙について学ぶようになりました。しかしその当初から『宇宙を研究しよう』と思っていたわけではありません。自分にできるか十分に自信がなかったのです。ただ、大学時代に必死に勉強する中で、宇宙は自分にも理解できる分野なんだと感じられるようになり、この道に進むことを決心しました」
宇宙を志すことを決めた柴田教授は、大学院から京都大学に進み宇宙物理学や一般相対論を研究する研究室(天体核研究室)に入る。そこで数値相対論に出合った。大学院時代に彼の指導にあたった中村卓史氏が、数値相対論を黎明期から引っ張ってきた人物だったのだ(先ほどの「BSSN形式」のNが中村氏だ)。そのもとで鍛えられた柴田教授は、すでに見てきたように、この分野でさまざまな貢献を果たし、数値相対論の発展に寄与してきた。
そしてついに、重力波がその姿を見せたのである。いま、柴田教授もその最前線で、これまで積み上げてきた成果を観測と照らし合わせる場面に来ているのだ。
「間もなく、いつ重力波の信号が届いても不思議ではない時代になるでしょう。そのときのために、数値相対論の研究者はできるだけ早く準備を進めなければなりません。つまり、観測された信号に対してなるべく正確かつ説得力のある説明が与えられるように事前にさまざまなシミュレーションをして準備しておくということです。それがいま、私たちにとっての喫緊の課題です」
重力波が次にいつ観測され、それがどのような事実を私たちに知らしめるのか。数値相対論はまさにこれから、数十年にわたって積み上げられてきた研究の成果を発揮するときなのである。

2016年に研究所に導入された新しいスーパーコンピュータシステム「Cray XC40」の前で。Crayの側面に描かれている写真は、本研究所設立のきっかけをつくった、湯川秀樹博士が教壇に立つ姿。Crayは日本全国の当該分野の研究者が利用できる。

http://www.yukawa.kyoto-u.ac.jp/
湯川秀樹博士のノーベル物理学賞受賞を記念して、1953年、日本初の全国共同利用研究所として創設。「素粒子論その他の基礎物理学に関する研究」を目的とする。1990年に広島大学理論物理学研究所と合併し、新基礎物理学研究所として再発足して現在に至る。
素粒子・原子核・宇宙・物性などの各分野の先駆的な研究で知られるとともに、全国の理論研究者たちの参画と協同のもと、全国的・国際的な共同研究や研究交流の一大拠点としても大きな役割を果たしている。
【取材・文:近藤雄生 / 撮影:水渡嘉昭】
 bana1.png (300px×80px)
bana1.png (300px×80px) bana1_e.png (300px×80px)
bana1_e.png (300px×80px) NovelPrize2015.png
NovelPrize2015.png